이번 글은 MARL 분야에서 MAAC로 유명한 ICML2019에 게재된 “Actor-Attention-Critic for Multi-Agent Reinforcement Learning” 리뷰 글입니다.
*AI Robotics KR 2024 Multi-Agent 스터디에서 발표한 내용입니다.
강화학습의 연구가 대부분 싱글 에이전트에 초점이 맞춰져 있는데, 리얼월드에서 실제 에이전트들은 동적으로 변화하는 환경에서 서로 다른 에이전트와 협력하거나 경쟁한다. 따라서 멀티에이전트 환경을 효과적으로 학습하기 위해서 에이전트는 환경의 동역학 뿐만 아니라 서로 다른 에이전트들의 관계도 파악해야 한다. 이번 논문은 이러한 멀티에이전트 환경을 효과적으로 학습하기 위해 에이전트가 서로의 partial observation을 공유한다는 특징을 처음으로 제안한 논문입니다.
1. Background
멀티에이전트 강화학습(MARL) 연구를 위한 가장 간단한 방법으로 다음과 같은 두 가지 방식이 있다.
1.
각각의 에이전트들이 독립적으로 개별 보상을 최대화하고 다른 에이전트들은 환경의 일부로 처리
2.
모든 에이전트들을 하나의 에이전트로 모델링해서 집단적인 행동을 가능하게 하는 방식
하나씩 살펴보자면,
•
각각의 에이전트들이 독립적으로 개별 보상을 최대화하고 다른 에이전트들은 환경의 일부로 처리하는 방식
첫 번째 방식의 경우, 환경이 stationary하고 markovian을 따른다는 강화학습의 기본 원칙을 위반한다. 강화학습에서 환경이 stationary하고 markovian하다는 가정은 환경의 동작이 일관되고 예측 가능해야 하며, 미래 상태는 오직 현재 상태에만 의존한다는 걸 의미한다.
참고. 강화학습에서 환경을 모델링할 때 기본적으로 가정하는 환경의 동역학 특성
그러나 MARL 환경에서는 에이전트의 정책이 변함에 따라 다른 에이전트의 환경도 시간에 따라 변한다. 즉 에이전트가 학습하는 동안 환경의 규칙이 지속적으로 변한다는 것을 의미하고, 이는 에이전트가 최적의 행동을 학습하고 예측하는 것을 어렵게 만든다. 따라서 MARL 환경은 에이전트들이 서로의 학습과정을 고려하여 협력하거나 경쟁하는 전략을 사용할 수 있고, 이를 통해 에이전트들이 환경 속에서 복잡한 동적 특성을 이해하고 적응하는 고급 전략 개발을 목표로 한다. 이런 동적 환경은 싱글 에이전트에 대해 non-stationary하게 작용하며 RL 기본 가정과 상충된다.
•
모든 에이전트들을 하나의 에이전트로 모델링해서 집단적인 행동을 가능하게 하는 방식
두번째 방식의 경우, 행동 공간은 모든 에이전트의 결합된 행동 공간이 된다. 이 방식은 에이전트 간의 협력적 행동을 가능하게 하지만, 에이전트 수에 따라서 행동 공간의 크기가 기하급수적으로 증가하게 되어 확장성에 문제가 생긴다.
1.1. Recent Works
MARL의 문제를 해결하기 위해 나온 기존 연구로 2017년 NeurIPS에 게재된 MADDPG와 2018년 AAAI에 게재된 COMA 연구가 있다. 이 두 연구는 모두 centralized critic 방식을 아래 그림과 같이 활용한다.
즉 centralized critic 방식은 (1)에이전트가 자신의 정책을 최적화 하는 동안 (2)critic이 전체 시스템의 성능을 평가하는 방식인데, 이 방식에도 두가지 발생 가능한 중요한 문제가 있다.
1.
Scalability — 확장성
2.
Generalization — 일반화
중앙집중화된 critic도 여전히 새로운 에이전트가 추가될 때마다 모든 에이전트의 행동과 상태를 고려해야 되고, 그 결과 에이전트의 수가 증가하는 경우, 학습해야 하는 상호 복잡성도 증가한다. 이는 확장성에 문제를 야기한다. 또한 특정 수의 에이전트에 대해 학습된 경우, 그 수가 변경되면 기존에 학습된 critic이 새로운 상황에 잘 적응하지 못할 수 있다. 이는 일반화에 문제를 야기한다.
이 논문는 이와 같은 문제를 해결하기 위해 Multi-Actor-Attention-Critic (MAAC) 기법을 제안하는데, 간단하게 설명하자면, 훈련 중 각 시점에서 어떤 에이전트에 주의(attention)를 기울일 지 동적으로 선택할 수 있는 모델을 제안한다. 이를 통해 에이전트 수 대비 입력 공간이 선형적으로 증가하게 되어 확장성 문제를 해결할 수 있었고, cooperative 뿐만 아니라 competitive, mixed 환경에서도 적용가능한 모델을 제안하면서 일반화 문제도 해결할 수 있었다.
본격적으로 논문이 제안하는 MAAC를 공부하기 전에 먼저 이해를 돕기 위해 Preliminaries를 살펴보고자 한다.
2. Preliminaries
2.1. Markov Games
Markov Decision Process의 multi-agent 개념에 해당한다.
•
a set of states,
•
action sets for each of agents,
•
a state transition function,
•
a reward function,
•
an observation,
•
global state,
•
a policy,
•
agent’s goal,
2.2. Policy Gradient
Policy gradient는 에이전트가 어떤 행동을 취했을 때 받을 수 있는 기대 리턴을 최대화하는 방향으로 정책 파라미터를 조정하는 방식이다. 여기서 는 정책 파라미터 에 대한 gradient 연산자이고, 는 정책을 따랐을 대, 기대할 수 있는 총 보상의 양을 의미한다. (*에이전트가 경험하는 모든 와 그 에서 취한 행동 를 통해 얻은 q보상 을 통해 정책 의 를 조정해서 기대 리턴값을 최대화하는 방향으로 정책 개선)
각 행동의 로그 확률의 gradient를 각 timestep마다 discount factor reward를 곱한 값들로 구성되는데, 이를 통해 정책의 파라미터를 조정해서 에이전트가 더 높은 보상을 기대할 수 있는 방향으로 학습하도록 유도한다.
2.3. Actor-Critic
Policy gradient 추정에서 합산한 은 에피소드 간에 리턴 값들이 극단적으로 변할 수 있기 때문에 높은 variance를 야기한다. Actor-Critic은 이 문제를 완화하기 위해 예상 리턴 값의 function approximation을 사용한다. Actor-Critic는 주어진 상태와 행동에 대한 expected discounted returns를 추정하는 함수 를 학습하는 것이다. 이는 off-policy temporal-difference learning 통해 아래 regression loss를 최소화하는 방향으로 학습된다.
참고. TD-Learning
이때 는 에 대한 타겟값으로, 에이전트가 장기적으로 더 많은 보상을 얻을 수 있는 방향으로 정책을 학습하도록 유도한다. 이러한 방법은 TD-Learning의 변형으로, 에이전트가 예측한 리턴값과 실제로 얻은 리턴값 사이의 차이를 최소화함으로, 에이전트의 정책과 가치 함수를 동시에 개선할 수 있다. (이때 는 타겟 Q-value function으로 과거 Q 함수들의 지수 이동 평균(exponential moving average)이다.)
참고. EMA
Actor-Critic은 Variance를 줄이고, 에이전트의 행동에 대한 보상을 좀더 정확히 추정하여 학습의 안정성을 향상 시킨다. 또한 타겟 Q-함수를 사용해서, 학습된 정책이 이전의 경험을 더 안정적으로 활용하게 되어, 성능 개선에도 도움이 된다.
2.4. Soft Actor-Critic
Soft Actor-Critic은 Actor-Critic의 policy gradient에 엔트로피항을 추가한 것으로, 에이전트가 단순히 보상을 최대화하는 것 외에도 더 많은 상태와 행동을 탐색하도록 한다. 즉 에이전트의 탐색을 장려하고 최적이 아닌 deterministic policy로 수렴하는 것을 피하기 위해 soft value function을 학습한다.
여기서 는 엔트로피 가중치로 탐색을 장려하고, 결정론적 행동을 억제하기 위해 사용된다. 정책의 무작위성을 증가시켜 에이전트가 새로운 상태와 행동을 탐색하도록 도와준다.
3. Multi-Actor-Attention-Critic (MAAC)
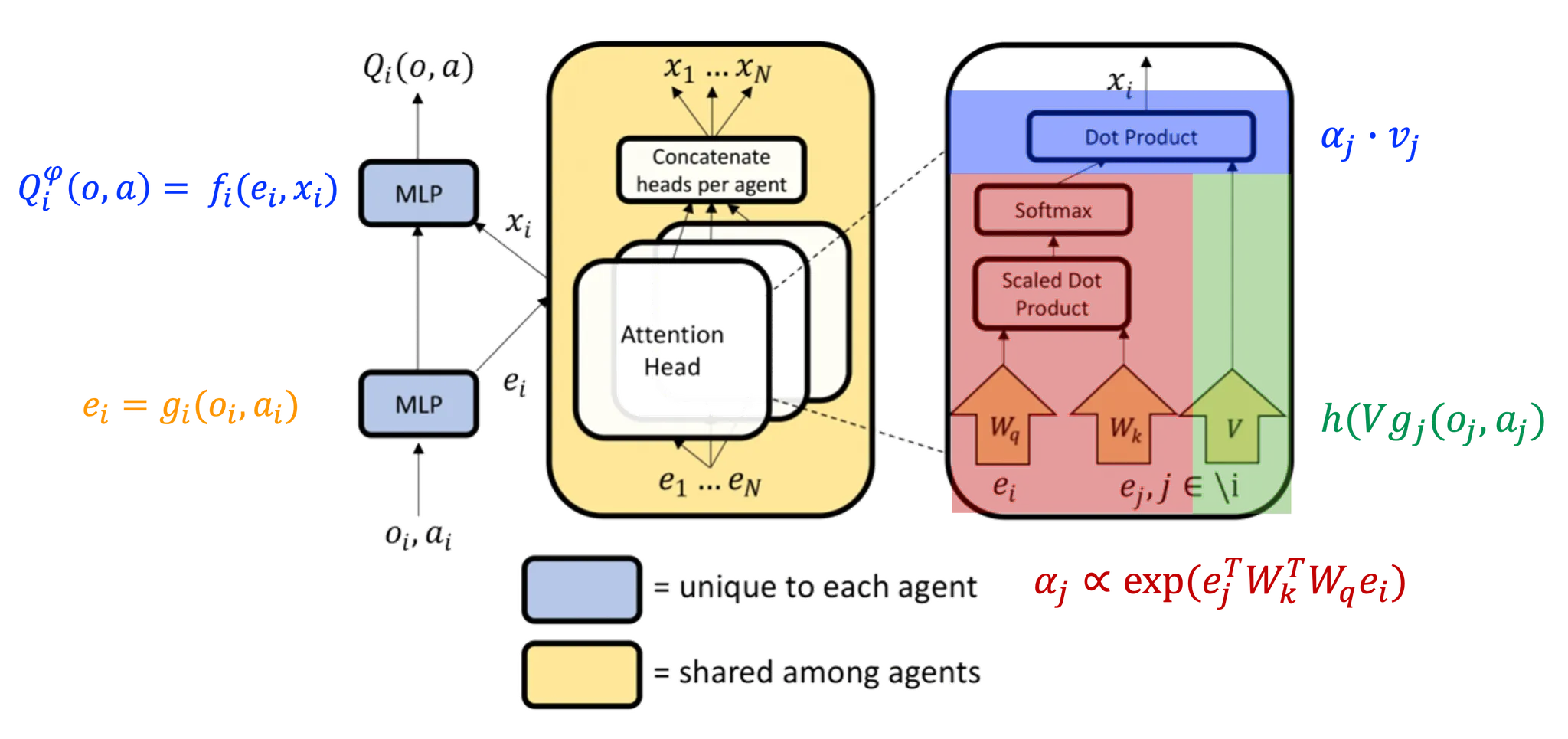
MAAC는 각 에이전트에 대한 critic을 학습하는데 있어, 다른 에이전트들의 정보에 선택적으로 주의를 기울이는 메커니즘을 사용한다. 이 방식은 중앙에서 critic을 학습하면서 non-stationary하고 non-markoivan 환경의 문제를 극복하고, 학습된 정책이 분산적으로 실행하는 것을 가능하게 한다. 간단하게 말하자면 앞에서 살펴본 Soft Actor-Critic에서 Critic Advantage에 Attention 모델을 활용하여 멀티에이전트 환경에 적용한 모델이다.
그럼 먼저 MAAC의 Attention 부분에 대해서 살펴보려고 한다.
3.1. Attention
Attention 메커니즘은 다른 에이전트들로부터의 정보를 선택적으로 추출하여 자신의 가치함수 추정에 활용하는 방식으로 작용한다. 즉 가변적인 Key-Value 메모리 모델을 기반으로 하며, 각 에이전트는 다른 에이전트들의 관찰과 행동에 대한 정보를 요청하고 그 정보를 자신의 가치 함수 추정에 통합한다. 즉 입력의 시간적, 공간적 근접성에 대한 가정은 하지 않는다. (why? 에이전트가 서로의 상태나 행동에 대한 정보를 수집할 때, 그 정보다 시간적 순서나 공간적 위치 기반에 중요하다고 가정하지 않는다. 즉, 에이전트가 관찰하고 행동하는 방식이 시간 및 공간에 구애받지 않고 독립적으로 중요할 수 있다고 보기 때문이다.)
참고. temporal or spatial locality
각 에이전트 의 Q-value function 은 에이전트의 관찰 과 행동 그리고 다른 에이전트들의 기여도 를 기반으로 계산된다. 각 에이전트의 기여도 는 다른 에이전트들의 가치 에 대한 가중치의 합으로, 여기서 는 에이전트 의 임베딩을 인코딩하고 공유된 행렬 에 의해 선형 변환된 값이다. 이때 는 element-wise non-linearity로 여기서는 Leaky ReLU를 사용한다.
참고. element-wise non-linearity
Attention weight 는 에이전트 에 대해 다른 에이전트 의 정보가 얼마나 중요한지. 즉, 각 에이전트 의 임베딩이 에이전트 에 의해 얼마나 주목받을 지 결정하는 가중치로 사용된다. 따라서 에이전트들의 상태와 행동 간의 관계를 모델링하고 중요한 정보에 더 많은 가중치를 부여해서 각 에이전트가 다른 에이전트들과 상호작용 속에서 최적의 행동을 결정하도록 돕는다. (는 우리가 이미 알고 있는 Transformer 모델의 Self-Attention으로부터 도출할 수 있다.)
이 논문의 경우, multi-head attention을 사용하는데, 이를 통해 에이전트 간의 상호작용에서 중요한 정보를 선택적으로 집중할 수 있는 능력을 넓히고 강화하게 된다. 각 attention head는 별도의 파라미터 ()를 사용해서 에이전트 에 대한 다른 모든 에이전트들의 기여도를 다르게 가중해서 계산하고, 최종적으로는 에이전트 에 대한 종합적인 표현을 생성할 수 있다. 따라서 에이전트는 동적이고 복잡한 환경에서 다른 에이전트들과의 상호작용을 더 세밀하게 조정할 수 있다.
에이전트 간의 critic 파라미터 공유를 통해 MAAC가 개별 에이전트에 대한 보상이 다르지만, 공통적인 피처를 공유하는 환경에서 효과적으로 학습할 수 있도록 한다. 이를 통해 모델이 일반화를 향상시킬 수 있도록 하며, 대립적인 상황에서도 효과적인 협력과 경쟁 전략을 학습할 수 있도록 한다.
참고. selectors (my opinion)
3.2. Learning with Attentive Critics
아래 식의 는 멀티에이전트 각각에 대한 손실함수로, 각 에이전트에 대해 예측된 Q-value 와 실제 리턴값 사이의 차이로 계산된다. (는 엔트로피와 보상 사이의 균형을 결정하는 파라미터이다.)
[Critic Update] 모든 critics은 파라미터 공유를 통해 joint regression loss function을 최소화하도록 함께 업데이트 된다. 이는 에이전트 에 대한 action-value estimator()가 관찰과 모든 에이전트의 행동을 받아들임으로, 모든 에이전트의 정보를 바탕으로 이루어진다.
[Policy Update] 개별 정책들을 다음과 같은 gradient ascent 를 통해 업데이트 된다. 모든 에이전트의 현재 정책에서 모든 행동을 샘플링해서 에이전트 에 대한 gradient 추정치를 계산한다. MADDPG와는 다르게, 다른 에이전트들의 행동 을 리플레이 버퍼 에서 샘플링하지 않고, 현재 정책 을 기반으로 샘플링해서, overgeneralization을 방지한다. 이때 는 advantage function을 계산하기 위해 사용되는 멀티 에이전트 baseline이다.
Critic 업데이트 과정에서 모든 에이전트 정보를 통합하고, 개별 정책 업데이트에서 현재 정책으로 부터 샘플링된 행동을 기반으로 gradient 추정을 수행하는데, 이를 통해 에이전트들이 현재 정책을 바탕으로 더 잘 협조할 수 있도록 설계되었다.
3.3. Multi-Agent Advantage Function
이 논문은 MARL의 credit assignment problem을 해결하기 위한 방법으로, Advantage Function 을 사용한다.
여기서 multi-agent credit assignment problem이란, 여러 에이전트가 함께 작업을 수행할 때 발생하는 문제이다. 각 에이전트는 환경에서 독립적으로 행동하며, 전체 시스템의 성능은 모든 에이전트의 결합된 행동에 의해 결정된다. 이러한 설정에서 개별 에이전트의 어떤 행동이 전체 그룹의 성공에 얼마나 기여했는지 결정하기 어렵다. 어떤 에이전트의 행동이 전체 보상에 얼마나 기여했는지를 알아내고, 이를 각 에이전트 학습에 반영하는 것이 중요하다.
이 문제 해결을 위해 본 논문에서는 Advantage function을 사용한다. Advantage function은 특정 에이전트의 행동이 평균적인 행동에 비해 얼마나 더 나은 결과를 가져오는 지를 측정하여, 각 에이전트의 행동이 전체 보상에 기여한 정도를 추정할 수 있게 한다. 이를 통해 개별 에이전트는 자신의 행동이 가져오는 결과에 대해 더 나은 결정을 내릴 수 있게 된다.
즉 는 특정 에이전트 의 행동이 주어진 상태 에서 얼마나 유리한지 평가한다.
이를통해 각 에이전트에 대해 다른 에이전트들로부터의 관련 정보에 동적으로 주의를 기울임으로, 에이전트 각각의 서로 다른 행동 공간을 가지고 있고, 전체 시스템이 전역 보상을 필요로 하지 않는 다양한 환경에 적용할 수 있는 멀티에이전트 학습 방법을 제공한다.
지금까지 살펴본 내용을 토대로 MAAC 모델의 훈련 절차 알고리즘을 살펴보면 다음과 같다.
1.
우선 병렬환경을 개의 에이전트와 함께 초기화하고, 리플레이버퍼도 초기화 한다.
2.
환경을 리셋하고, 각 에이전트 에 대한 초기 관측 를 얻는다
3.
에이전트 에 대해 정책 를 사용해서 행동 를 선택한다.
4.
선택된 행동을 모든 병렬 환경에 전송하고, 모든 에이전트의 새 관측 와 보상 를 얻는다.
5.
모든 환경에 대한 transition을 리플레이 버퍼에 저장한다.
6.
[Critic Update] 리플레이 버퍼에서 미니배치 를 샘플링한다.
7.
[Critic Update] critic update 함수를 통해 critic을 업데이트 한다.
8.
[Policy Update] 리플레이 버퍼에서 여러 관측 을 포함하는 미니배치를 샘플링한다.
9.
[Policy Update] policy update 함수를 통해 정책을 업데이트 한다.
10.
타겟 파라미터 와 를 업데이트 한다.
4. Experiments
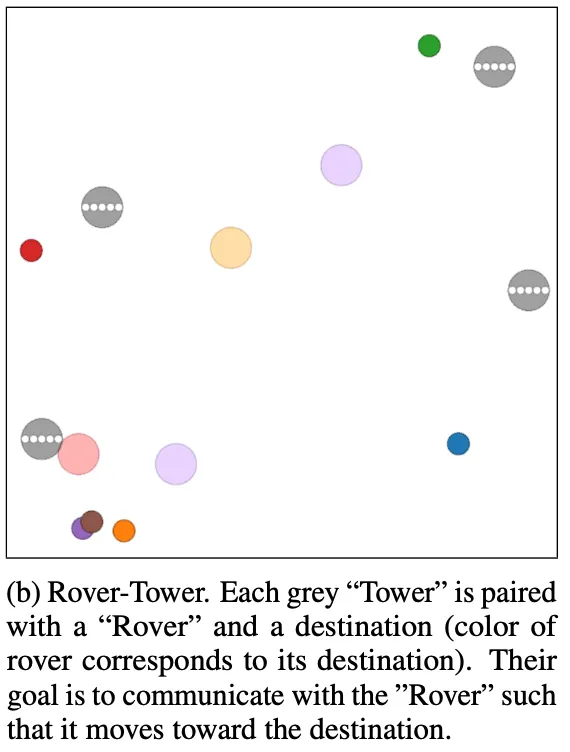
MAAC를 실험한 환경은 (1) Cooperative Treasure Collection(CTC)와 (2)Rover-Tower(RT) 두가지 이다. CTC는 아래 왼쪽 그림을 통해 알 수 있듯, 6개의 hunter와 2개의 bank 총 8개의 에이전트로 이루어져있다. hunter는 treasure를 모으고, bank에 treasure를 보낸다. RT는 한 쌍으로 이루어진 rover와 tower가 있고, rover는 tower 정보만을 가지고 목표로 이동한다. tower는 탐사 로봇을 포함하여 목적지를 찾을 수 있고 쌍으로 이루어져 있는 탐사 로봇에게 상/하/좌/우/정지 5개의 메시지를 보낼 수 있다.
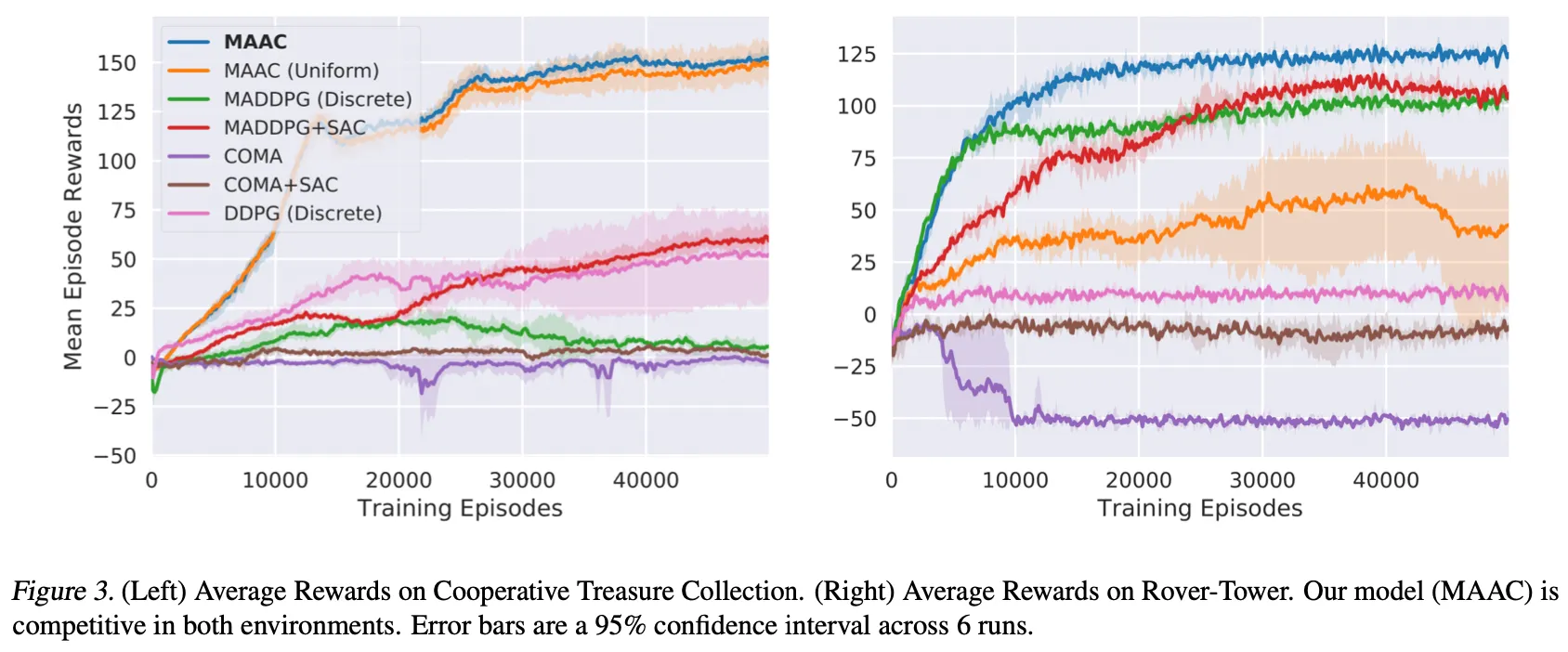
다음은 멀티에이전트 기존 연구들과 비교한 결과를 나타내는 그래프이다. 이때 MAAC(uniform)은 attention score를 동일한 비율로 적용한 결과를 뜻한다. MAAC는 CTC와 RT 모두에서 좋은 결과를 보여주는데, MAAC(uniform)의 경우, RT에서 성능이 대폭 하락한다. 이를통해 RT 실험이 attention model이 어떤 효과를 보여주는 지 입증하는 실험이라는 걸 알 수 있다.
MADDPG의 경우 에이전트에 따라 큰 관찰 공간을 가져야 하기 때문에 CTC 환경에서 안좋은 결과를 보여주고, COMA의 경우 비슷한 행동 공간을 가지는 경우에 좋은 결과 야기하는 것을 알 수 있다.
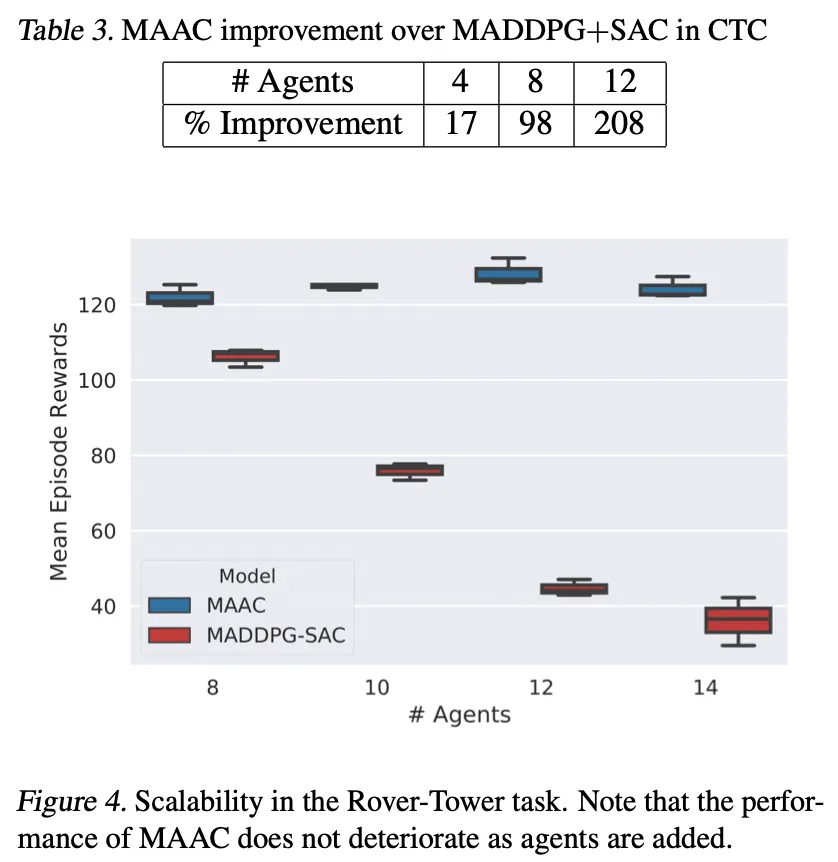
다음 표는 에이전트가 증가함에 따른 실험결과를 MADDPG+SAC와 비교한 표이다. MAAC는 에이전트가 증가함에 따라 성능이 비슷하거나 좋아지지만, MADDPG+SAC의 경우, 에이전트 수가 증가할 수록 성능이 떨어지는것을 알 수 있다.
이번 글에서는 Actor-Attention-Critic for Multi-Agent Reinforcement Learning 논문을 살펴보았다. 논문에서 제안하는 MAAC는 멀티에이전트에서 중앙집중식 critic 기법의 확장성 및 일반화 문제를 해결하기 위해 제안된 기법으로, multi-head attention으로 critic advantage를 계산해서 실제 환경에서 에이전트가 어떤 에이전트에 주의를 기울여야 하는지 알 수 있고, 학습하는 동안 매 timestep 마다 어떤 에이전트에 주의를 기울일 지 동적으로 선택할 수 있는 방식을 제안하고 있다.