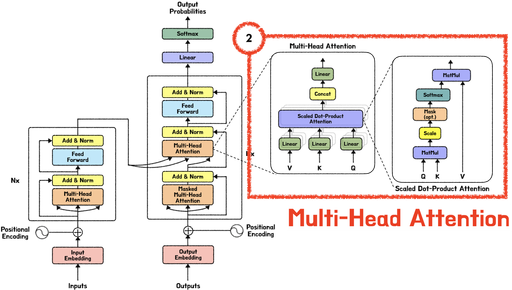
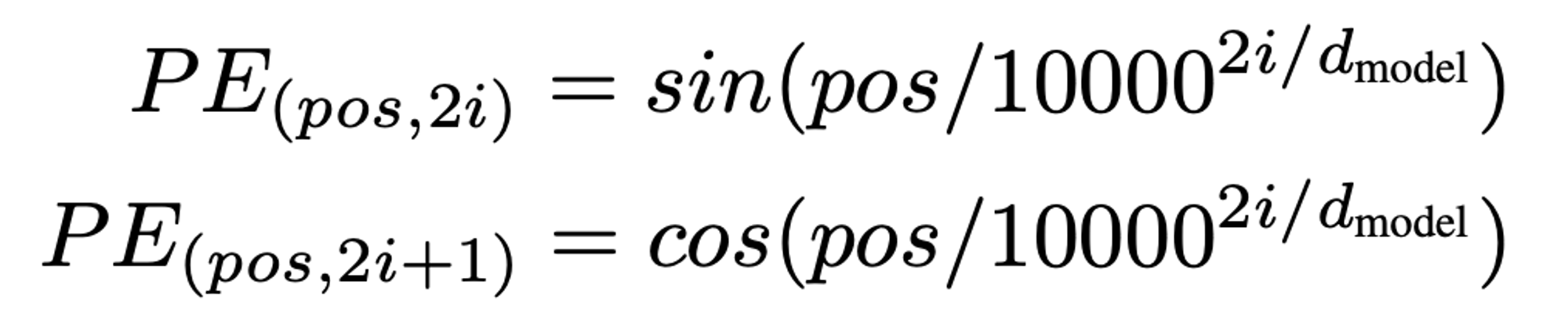트랜스포머 논문. Transfomer: “Attention is All You Need” 내용 중 Positional Encoding에 대해 공부한 내용을 정리하였습니다.
트랜스포머 — 아키텍처 by minkyung(blossomindy)
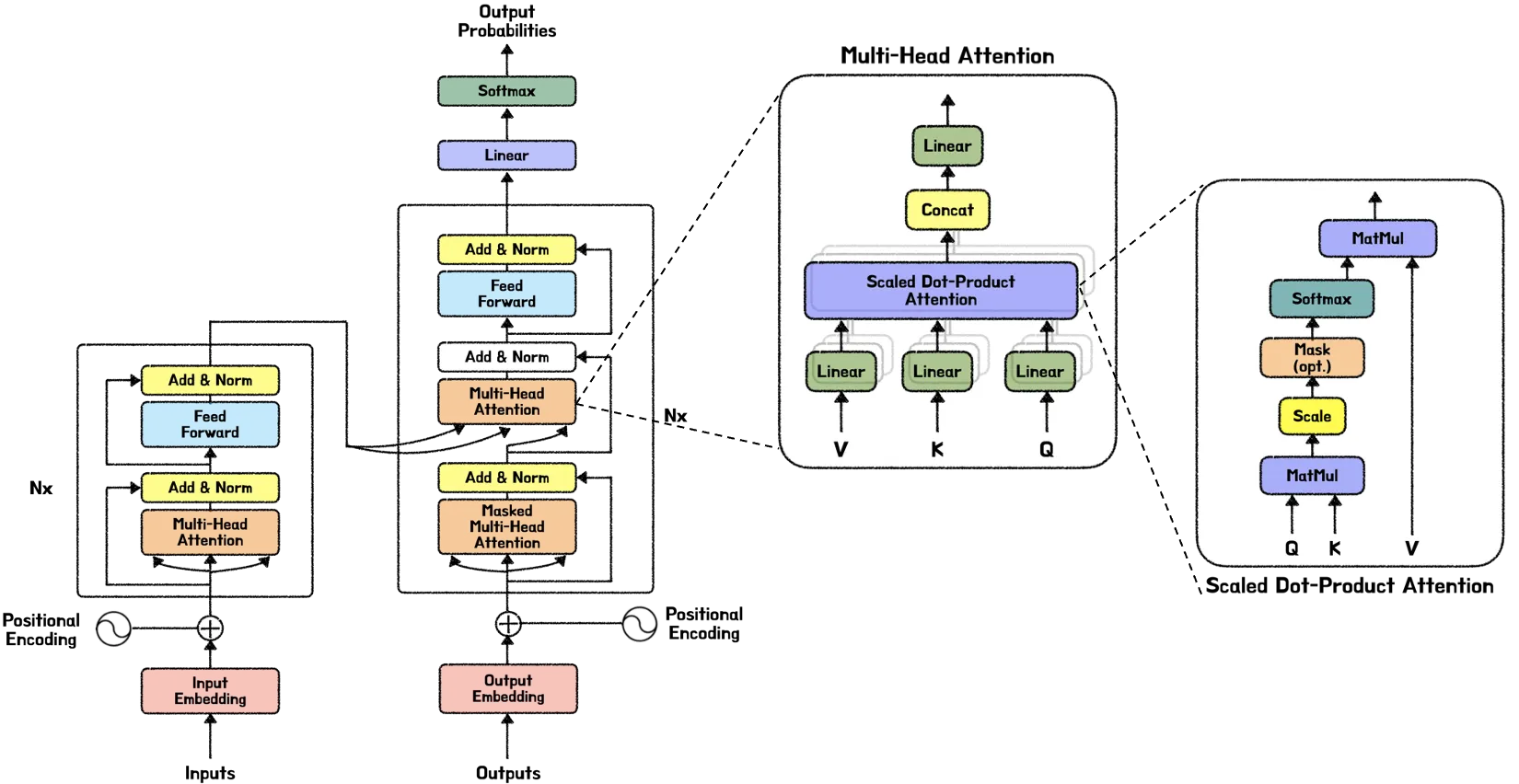
트랜스포머가 딥러닝 세상을 지배한다는 말이 나올 만큼 트랜스포머는 자연어처리와 비전 분야에서 각광을 받으며 굳건히 SOTA(state-of-the-art)의 자리를 지켜오고 있습니다. 따라서 제대로 공부하자는 의미에서 “Attention is All You Need” NIPS 2017 논문 리뷰를 합니다. 논문 리뷰는 단순 번역이 아닌 트랜스포머를 깊게 파헤쳐보자는 취지로 트랜스포머 아키텍처를 각각의 파트 별로 나눠서 작성할 계획입니다.
이번 글은 트랜스포머 깊게 공부하기 첫 시작으로 “Positional Encoding”에 대해 공부한 내용을 정리했습니다.
1. Input Embedding
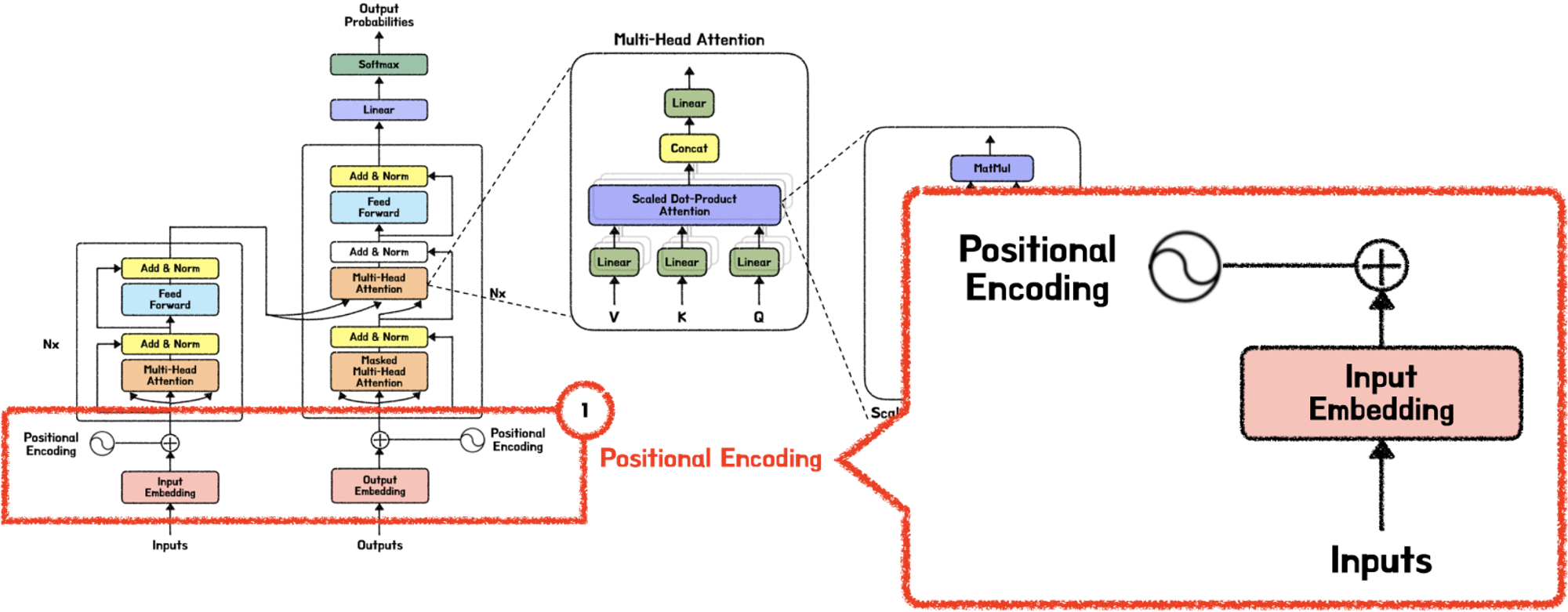
Input Embedding은 Input에 입력된 데이터를 컴퓨터가 이해할 수 있도록 행렬 값으로 바꾸어 준다.
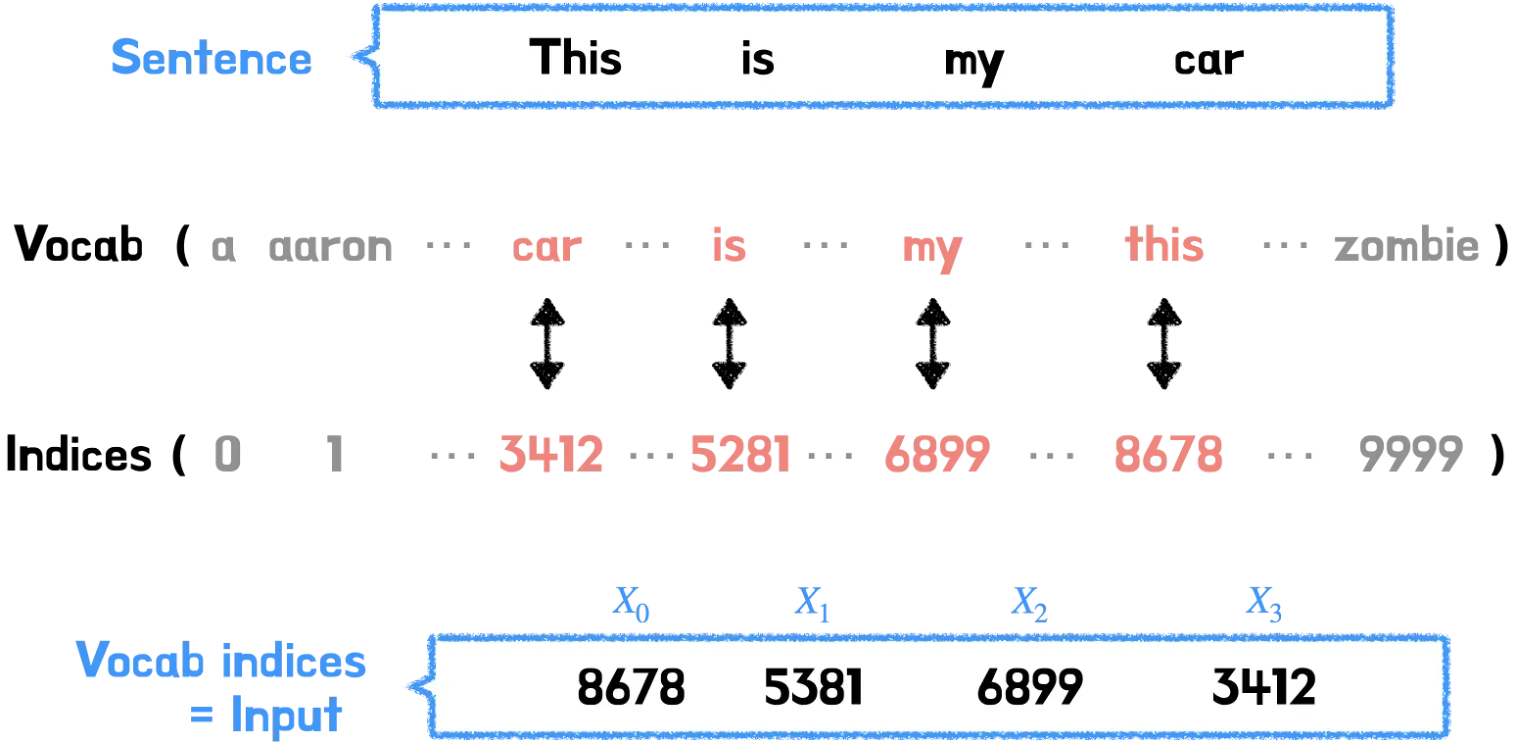
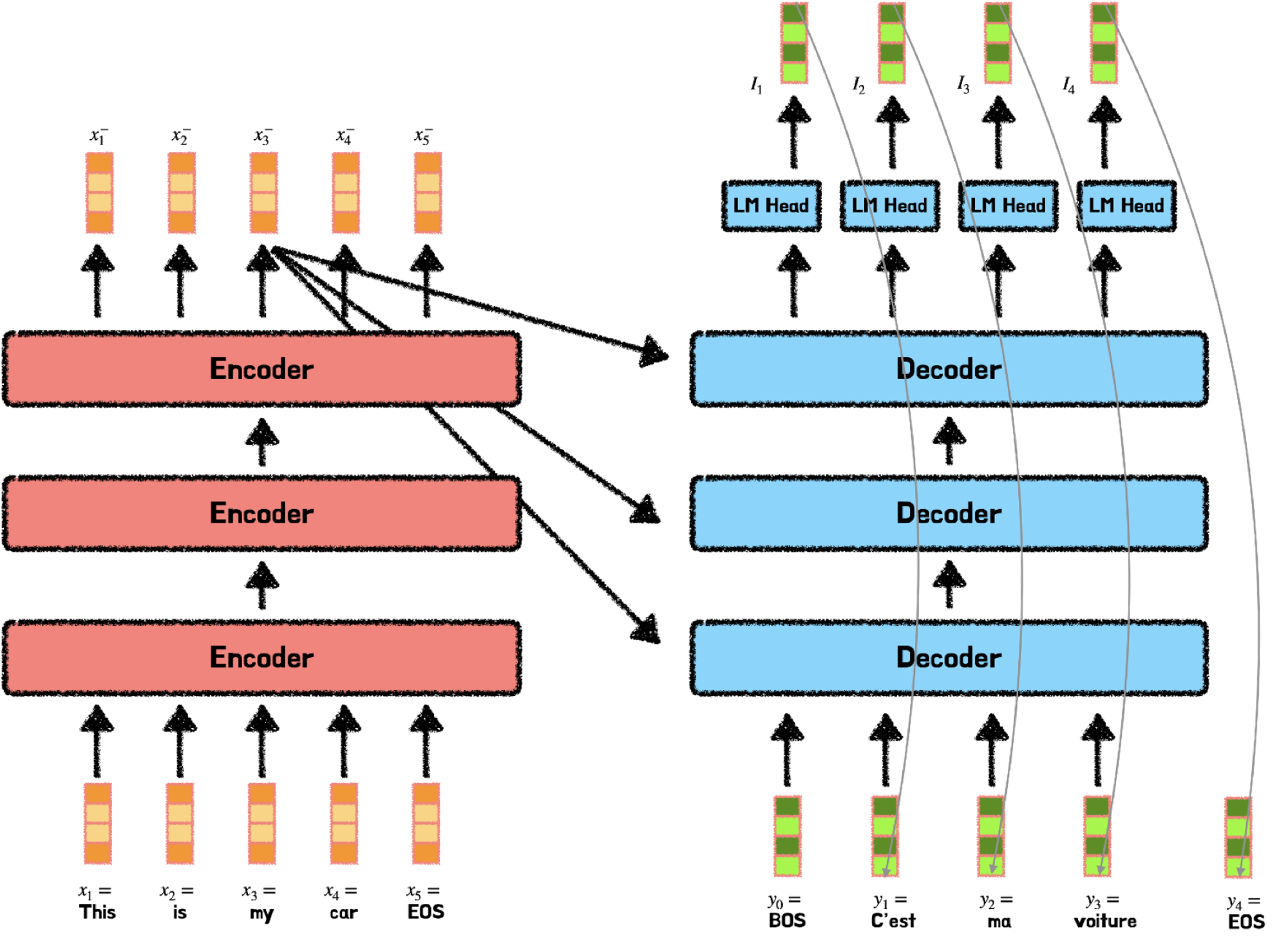
예를 들어 설명하자면, “This is my car” 라는 문장이 주어졌을 때, 문장을 구성하는 각각의 단어는 그에 상응하는 인덱스 값에 매칭이 되고, 이 인덱스 값들은 Input Embedding에 전달된다.
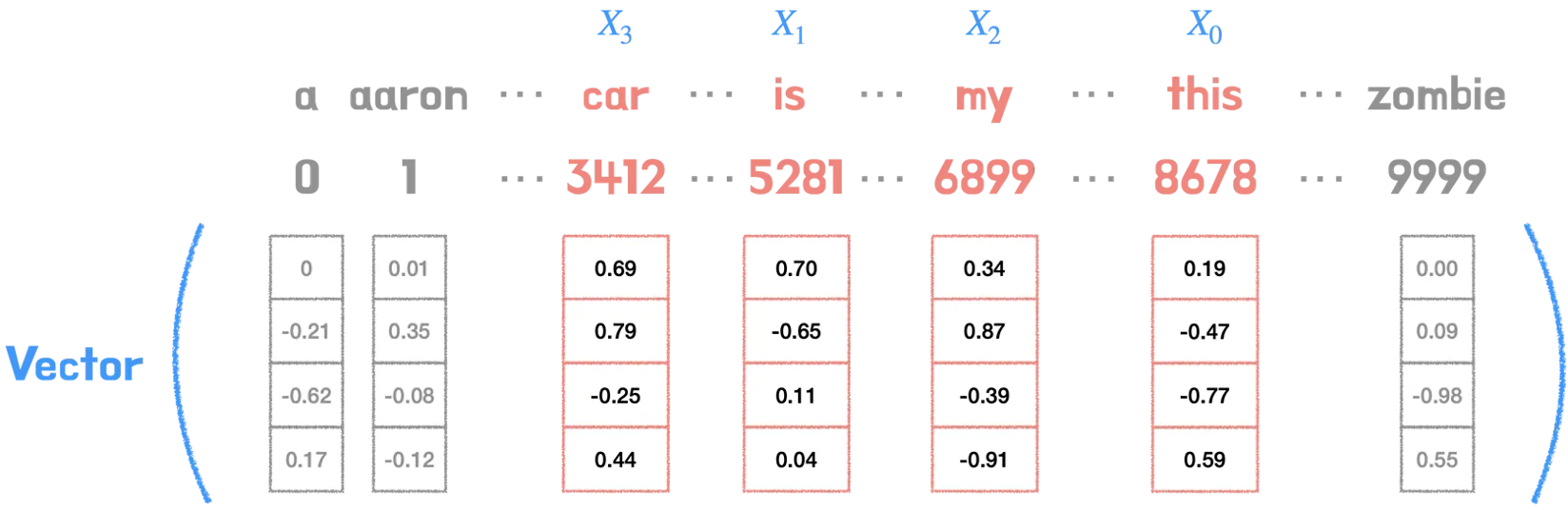
이때 각각의 단어 인덱스들은 저마다 다른 벡터값을 지니고 있다.(그림에서는 이해하기 쉽게 임베딩 크기를 4로 했지만 실제 논문 상 임베딩 크기는 512이다.) 이때 각각의 벡터 차원은 해당 단어의 피처 값을 가지고 있고, 서로 다른 단어의 피처 값이 유사할 수록 벡터공간의 임베딩 벡터는 점점 가까워질 것이다.
위 그림을 예를 들어 설명하자면, car와 this 두 단어의 벡터 값을 벡터공간에 나타냈을 때, 서로 다른 두 단어가 공유하는 피처값이 존재하고 문맥상 유사도가 높다면, 임베딩 벡터값은 점점 가까워질 것이다. 반면에 zombie의 경우, 공유하는 피처값이 없고 문맥상 유사도도 낮아서 임베딩 벡터값은 가까워지지 않는다.
이처럼 임베딩 레이어는 Input 인덱스 값들을 받아서 이를 각각의 단어 임베딩 벡터값으로 바꿔준다. 그후 단어 임베딩 벡터값에 Positional Encoding의 벡터값을 더하는 연산을 하게 되는데, 그 전에 트랜스포머의 특징이 무엇이고, 따라서 Positional Embedding 값이 왜 필요한지에 대해 설명하고자 한다.
2. Transformer 특징: Sequential? Parallel?
트랜스포머 이전에는 RNN과 LSTM으로 구성된 방법들이 주로 사용되었는데, 이들은 순차적으로 문장을 처리하는 특징을 지니고 있다. 즉 Input에 입력되는 순서대로 RNN 또는 LSTM 모델 내에서 처리가 되는 방식을 말한다. 다시 말해 앞의 연산이 끝나야 뒤의 연산을 진행할 수 있다. 따라서 계산 유닛이 많아도 한번에 1개씩 처리가 된다. 이 경우 발생하는 문제는 연산 속도가 매우 느리다는 점이다.
하지만 RNN이나 LSTM과는 다르게, 트랜스포머의 경우 입력되는 문장을 순차적으로 처리하지 않는다. 대신 트랜스포머는 입력된 문장을 병렬로 한번에 처리한다는 특징을 지니고 있다.
따라서 트랜스포머처럼 병렬로 값을 처리하면 연산을 훨씬 더 빠르게 수행할 수 있다. 하지만 단어의 위치(순서)를 알 수 없다는 문제가 발생한다. 이 문제를 해결하기 위해 논문에서 Positional Encoding을 제안한다.
3. Positional Encoding
앞에서 간단하게 언급한 것처럼 트랜스포머는 입력된 데이터를 한번에 병렬로 처리해서 속도가 빠르다는 장점이 있다. 하지만 RNN과 LSTM과 다르게 트랜스포머는 입력 순서가 단어 순서에 대한 정보를 보장하지 않는다. 다시 말하면, 트랜스포머의 경우 시퀀스가 한번에 병렬로 입력되기에 단어 순서에 대한 정보가 사라진다. 따라서 단어 위치 정보를 별도로 넣어줘야 한다. 그렇다면 단어의 위치 정보는 왜 중요하고, 논문에서는 이 문제를 Postional Encoding으로 어떻게 해결하고 있을까?
3.1. 단어의 위치 정보가 중요한 이유
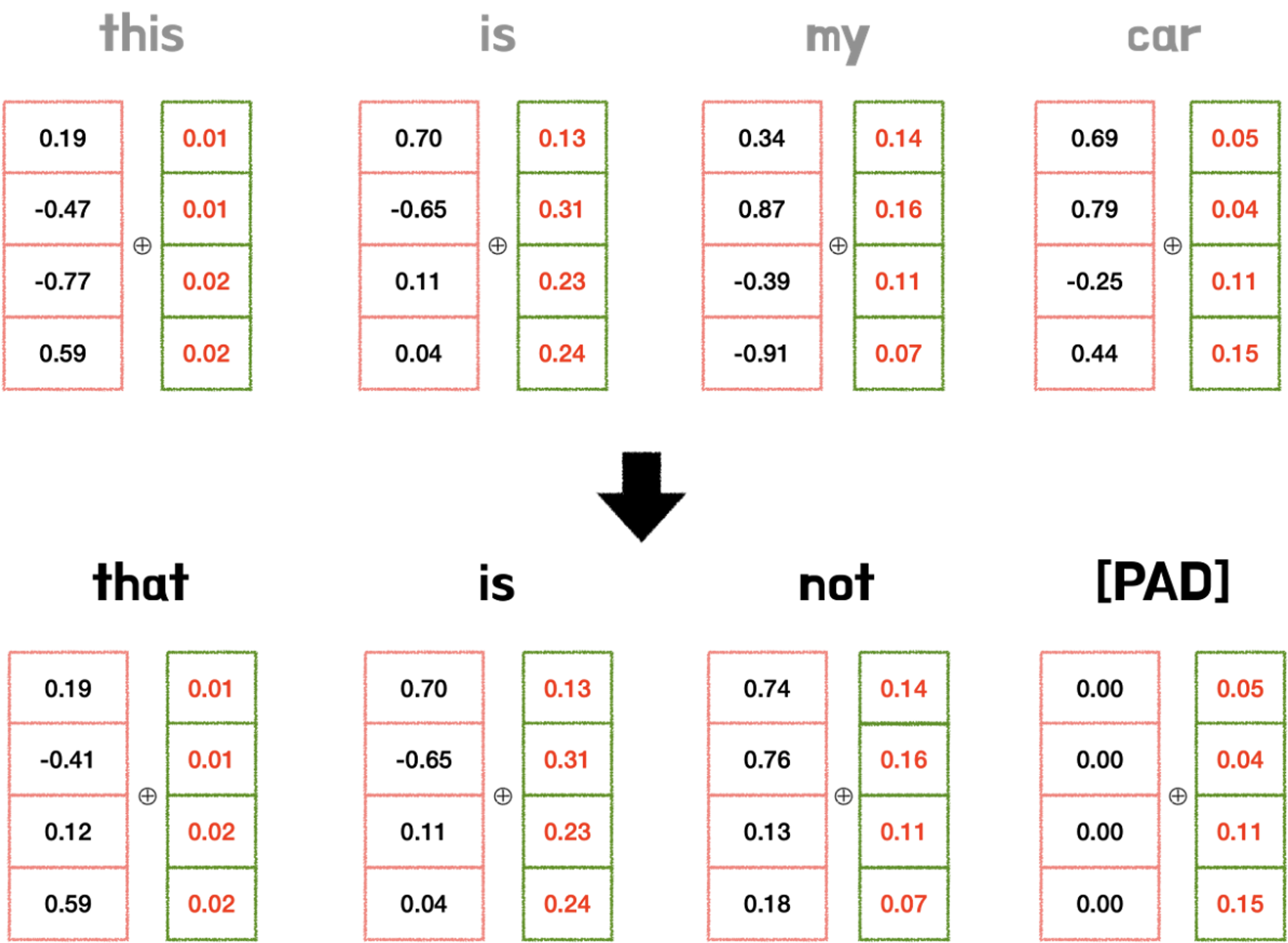
위 두 문장을 해석해보면, 1번 문장은 “지난 토플시험에서 95점을 못 받았지만, 박사과정에 입학할 수 있었다”이고, 2번 문장은 “지난 토플 시험에서 95점을 받았지만, 박사과정에 입학하지 못했다"가 된다. NOT의 위치 차이로 인해 두 문장의 뜻이 완전히 달라져버렸다. 이와 같이 문장 내의 정확한 단어 위치를 알 수 없다면 문장의 뜻이 완전히 달라지는 문제가 발생할 수 밖에 없다.
따라서 그림과 같이 각각의 단어 벡터에 Positional Encoding을 통해 얻은 위치정보를 더해줘야 된다. 이때 반드시 지켜야 될 규칙 두 가지가 있다.
1.
모든 위치값은 시퀀스의 길이나 Input에 관계없이 동일한 식별자를 가져야 한다. 따라서 시퀀스가 변경되더라도 위치 임베딩은 동일하게 유지될 수 있다.
2.
모든 위치값은 너무 크면 안된다. 위치값이 너무 커져버리면, 단어 간의 상관관계 및 의미를 유추할 수 있는 의미정보 값이 상대적으로 작아지게 되고, Attention layer에서 제대로 학습 및 훈련이 되지 않을 수 있다.
3.2. 위치 벡터를 얻는 두 가지 방법과 문제점
위치 벡터를 부여하는 방법으로는 다음과 같이 간단한 두 가지 방법을 떠올릴 수 있다.
1.
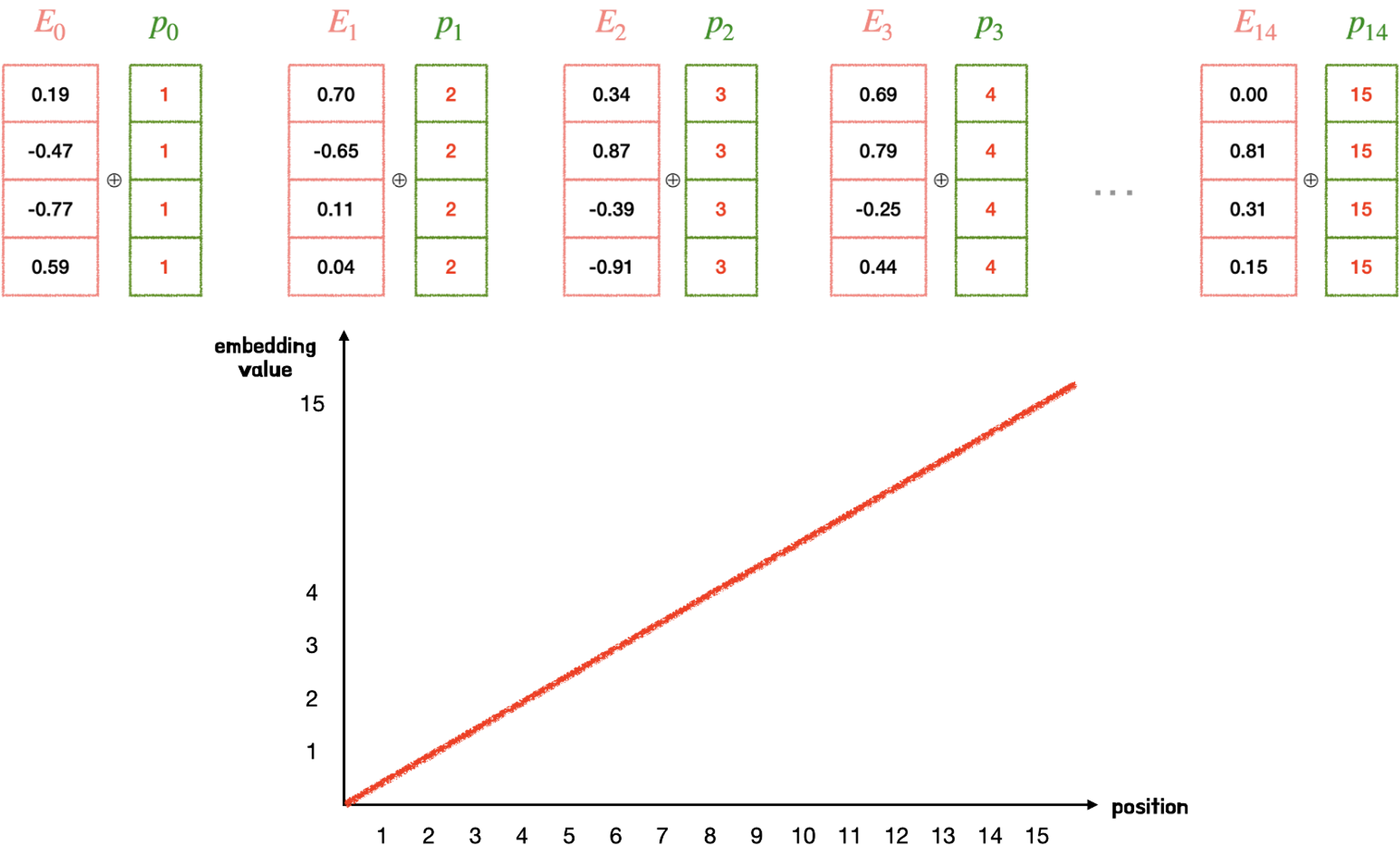
첫 번째 토큰에는 1, 두 번째 토큰은 2, 세 번째 토큰은 3… 등등 시퀀스 크기에 비례해서 일정하게 커지는 정수값을 부과할 수 있다.
하지만 그림과 같이 위치 정보 값이 급격히 커지면 단어 벡터와 더했을 때, 단어보다 위치 정보가 지배적이라 단어의 의미가 훼손될 수 있다. 즉 이와같은 경우, 시퀀스 길이가 커질 수록 위치 벡터 값 또한 점점 커진다는 문제점이 있고, 위치 벡터가 특정한 범위를 갖고 있지 않아서 모델의 일반화 역시 불가능해진다.
2.
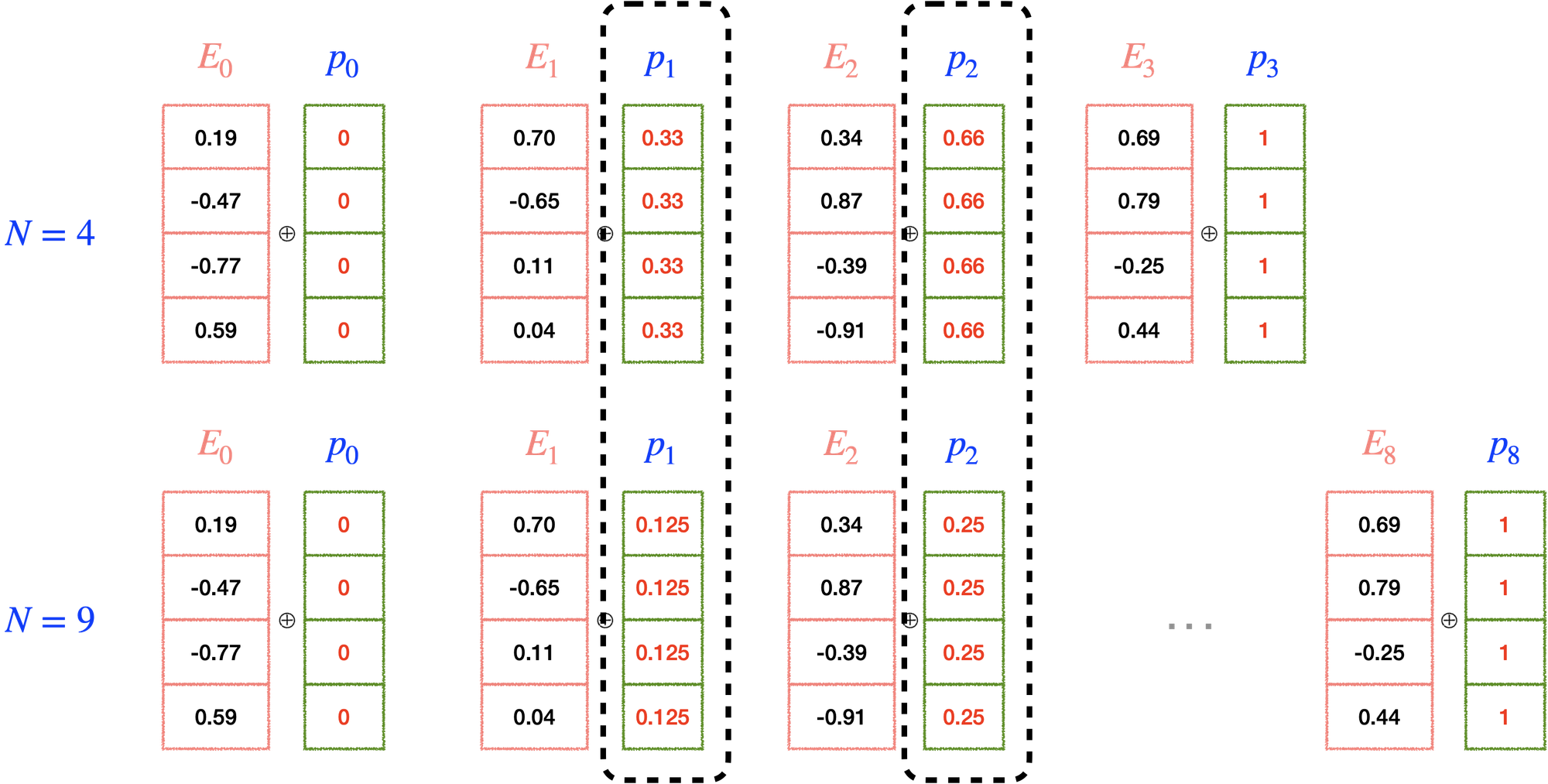
첫 번째 토큰에는 0, 마지막 토큰은 1을 부과하고, 그 사이를 (1/단어수)로 나누어 나온 값(normalizatoin)을 적용해 볼 수 있다.
하지만 이 경우 같은 시퀀스 길이에 따라서 같은 위치 정보에 해당하는 위치 벡터값이 달라질 수 있고, 시퀀스의 총 길이도 알 수 없다. 바로 옆에 위치한 토큰들 간의 차이(단어 레이블 간의 차이) 역시 달라지는 문제점이 존재한다.
따라서 앞서 언급한 것처럼 단어 의미정보가 변질되지 않도록 위치 벡터값이 너무 커서도 안되고, 같은 위치의 토큰은 항상 같은 위치 벡터값을 가지고 있어야 한다.
3.3. Positional Encoding을 위한 Sine & Cosine 함수
이 두 가지 규칙을 지키면서 위치 벡터를 부과하는 방법에는 sine & cosine 함수가 있다. 그런데 정말 sine & cosine 함수가 positional encoding의 모든 조건에 딱 맞아 떨어질까?
1.
의미정보가 변질되지 않도록 위치 벡터값이 너무 크면 안된다.
→ sine & cosinee 함수는 -1 ~ 1 사이를 반복하는 주기함수이다. 즉 1을 초과하지 않고 -1 미만으로 떨어지지 않으므로 값이 너무 커지지 않는 조건을 만족 시킨다.
2.
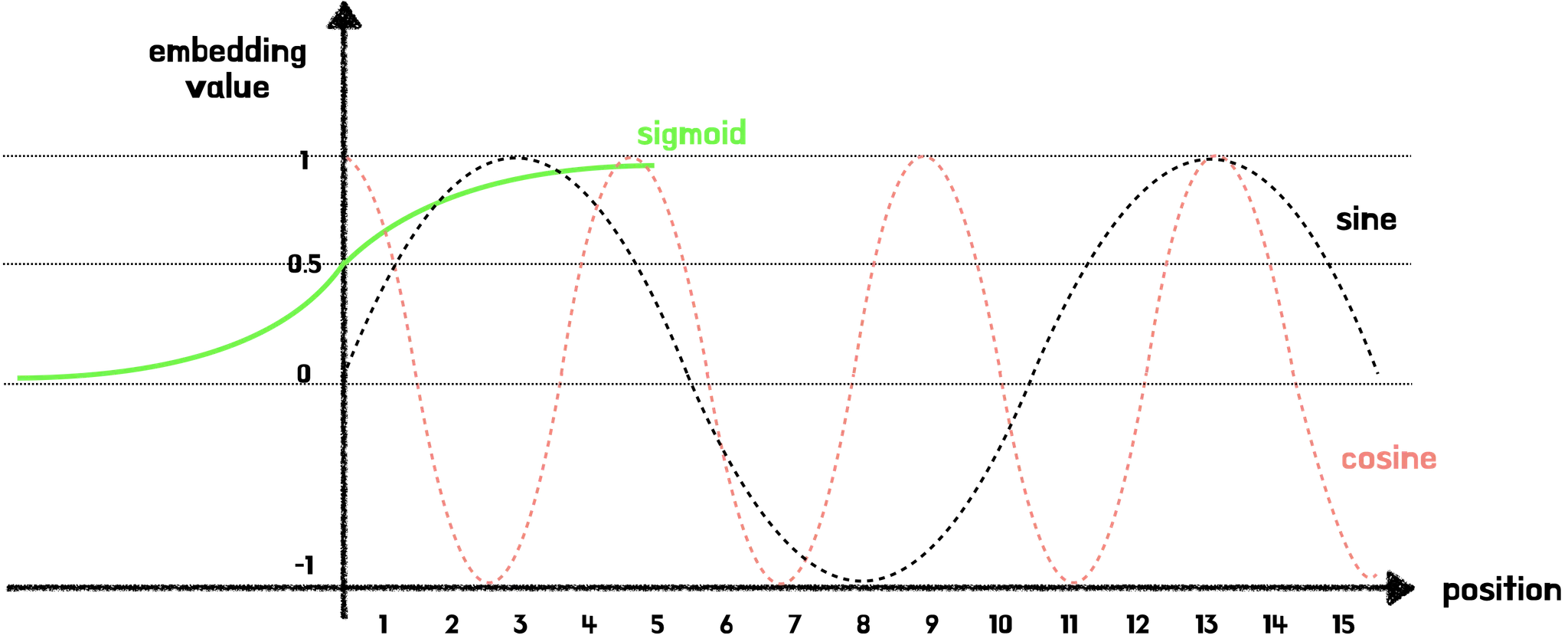
sine & cosine 함수 외에도 일정 구간 내에 있는 함수로는 Sigmoid 함수가 있다. 그런데 왜 sine & cosine 함수를 선택했을까? sine & cosine 함수는 앞서 언급한 것처럼 주기함수이기 때문이다.
→ Simoid 함수의 경우, 긴 문장의 시퀀스가 주어진 경우, 위치 벡터값의 차가 미미해지는 문제가 발생할 수 있다. 하지만 sine & cosine 함수의 경우 -1 ~ 1 사이를 주기적으로 반복하기에 긴 문장의 시퀀스가 주어진다 해도, 위치 벡터값의 차가 작지 않게 된다.
3.
같은 위치의 토큰은 항상 같은 위치 벡터값을 가지고 있어야 한다. 하지만 서로 다른 위치의 토큰은 위치 벡터값이 서로 달라야 한다. 문제는 -1 ~ 1 사이를 반복하는 주기함수기 때문에 토큰들의 위치 벡터값이 같은 경우가 생길 수 있다.
예를 들어 아래 그림과 같이 Sine 함수가 주어진다면 1 번째 토큰(position 0)과 9 번째 토큰(position 9)의 경우, 위치 벡터값이 같아지는 문제가 발생한다.
→ 하지만 여기서 우리가 놓치지 말아야 될 positional encoding의 또 다른 특징이 있다.
•
positional encoding은 스칼라값이 아닌 벡터값으로 단어 벡터와 같은 차원을 지닌 벡터값이다.
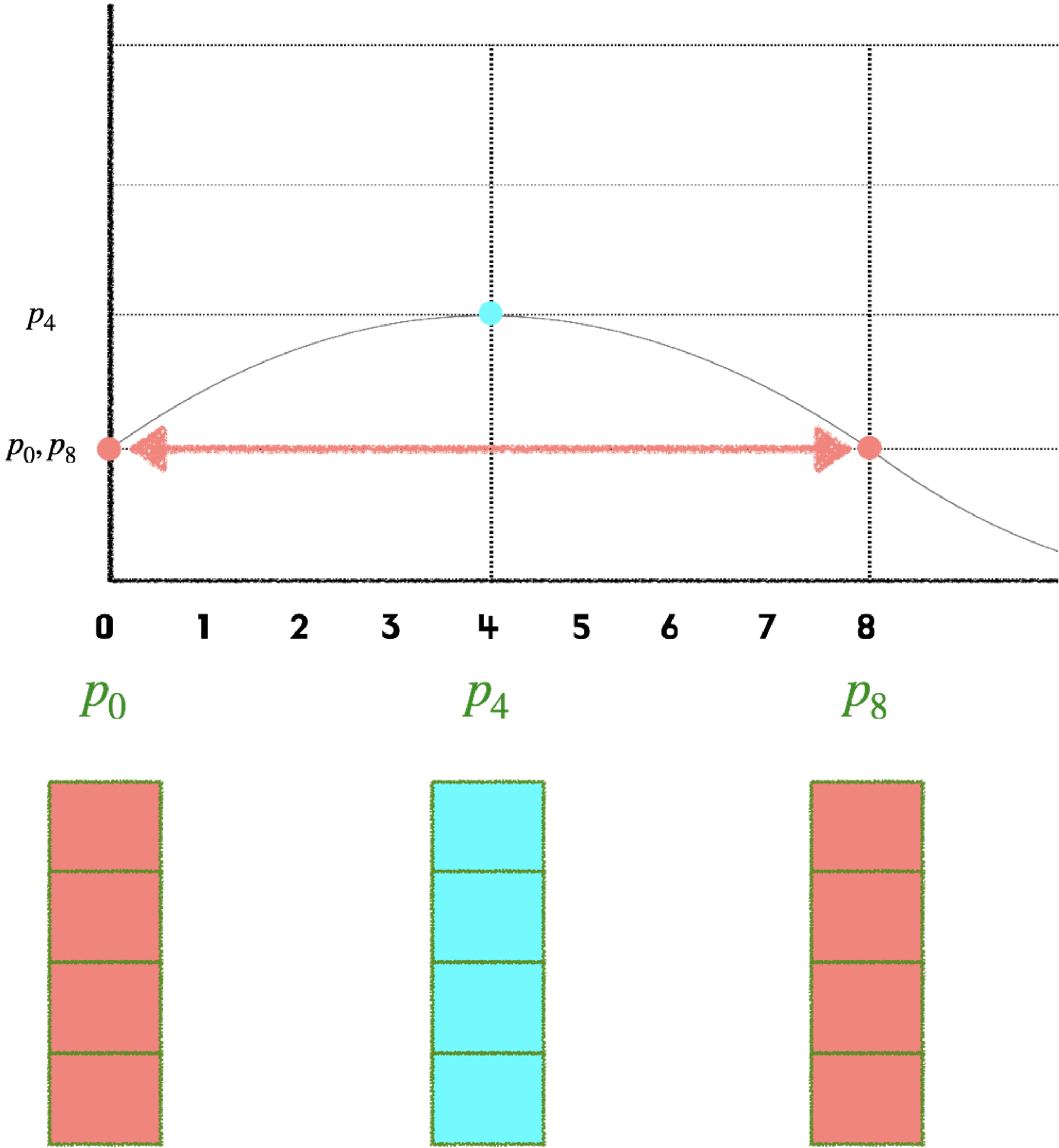
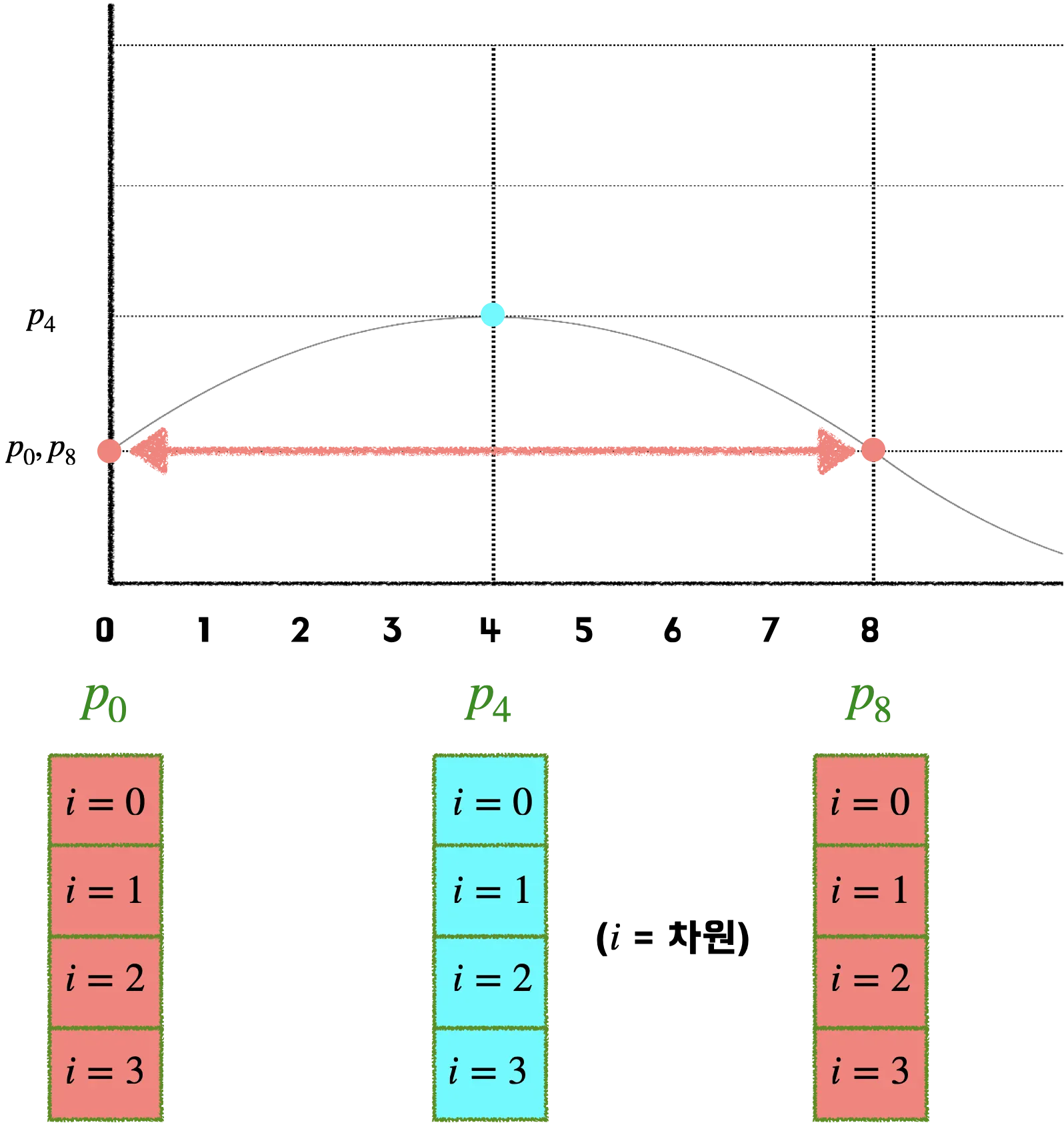
따라서 위치 벡터값이 같아지는 문제를 해결하기 위해, 다양한 주기의 sine & cosine 함수를 동시에 사용한다. 하나의 위치 벡터가 4개의 차원으로 표현된다면, 각 요소는 서로 다른 4개의 주기를 갖게 되기 때문에 서로 겹치지 않는다. (물론 모든 주기의 공배수만큼 지난 위치는 겹칠 수 있겠지만, 그 정도면 이미 대부분의 단어 위치를 표현할 수 있다.) 즉 단어 벡터는 각각의 차원마다 서로 다른 위치 벡터값을 가지게 된다.
위 그림처럼 첫 번째 차원의 벡터값들의 차이가 크지 않다면, 단어 벡터의 다음 차원에도 벡터값을 부여하면 된다. 이때 동일한 sine 값을 사용하게 되면, 벡터들 간의 차가 크지 않게 되므로, cosine 값을 사용한다. 하지만 두 번째 차원의 벡터값들 역시 그 차가 크지 않다면, 서로 다른 단어 벡터 간의 위치 정보 차이가 미미하게 된다. 이 경우 cosine의 frequency를 이전 sine 함수보다 크게 주면되고, 마지막 차원의 벡터값이 채워질 때까지 서로 다른 frequency를 가진 sine & cosine을 번갈아가며 계산하다 보면 결과적으로 충분히 서로 다른 positional encoding 값을 지니게 된다. 이를 수식으로 표현하면 아래와 같다.(이때 pos는 position, i는 차원을 의미한다.)
4. Input Embedding과 Positional Encoding 간의 연산
4.1. Concatenate 대신에 Summation 연산을 사용했을까?
위 과정을 통해 얻게 된 단어 벡터와 위치 벡터값은 다음 레이어로 가기 전에 연산과정 Summation을 거친다. 여기서 왜 Concatenate이 아닌 Summation 연산을 사용했을까?
위 그림은 Concatenate을 사용한 경우이다. Concatenate를 사용하면 단어 의미 정보를 포함하고 있는 단어 벡터 뒤에 위치 정보를 포함하는 positional embedding이 연결된다. 이 경우 단어의 의미 정보는 자체 차원 공간을 갖게 되고, 위치 정보 역시 자체 차원 공간을 갖으며, 직교성질(orthogonal)에 의해 둘은 서로 전혀 관계없는 공간에 있게 된다.
이러한 Concatenate가 주는 이점은 정보가 뒤섞이는 혼란을 피할 수 있게 해주지만, 메모리, 파라미터, 런타임 등과 관련된 비용 문제가 발생한다.
Summation을 사용한다면, 단어 의미 정보와 위치 정보 간의 균형을 잘 맞출 수 있다. 즉 모델이 위치 정보를 적절하게 가지게 되고 동시에 단어 의미 정보 역시 충분히 강력하게 유지되어 벡터 공간에서 단어 의미 정보와 위치 정보 간의 거리가 적절해진다. 하지만 Summation의 경우, 정보가 뒤섞이는 문제가 발생할 수 있다. 따라서 모델이 매우 크고 GPU 등의 성능이 좋고 비용 문제가 발생하지 않다면 Concatenate을 사용해도 무관하다.
트랜스포머 논문이 처음 발표됐던 2017년도만 해도 GPU 등 컴퓨팅 파워가 지금만큼 좋지 않았다. 따라서 당시 저자들이 Concatenate 대신 Summation을 단어 벡터와 위치 벡터 간의 연산으로 선택했다고 생각된다.
이번 글에서는 트랜스포머 “Attention is All You Need” 논문 중 Postional Encoding 부분에 대한 내용을 정리했습니다. 트랜스포머 모델에서는 Postional Encoding 덕분에 병렬로 한번에 다량의 단어 벡터들을 처리할 수 있다는 사실을 알게되었습니다.
다음 글에서는 “트랜스포머: Muti-head Attention”에 대해 깊게 공부한 내용을 정리할 예정입니다.
5. 참고자료
[2] Dzmitry Bahdanau et al. “Neural Machine Translation by Jointly Leraing to Align and Translate”, ICLR 2015
[3] Minh-Thang Luong et al. “Effective Approaches to Attention-based Neural Machine Translation”, EMNLP 2015
•
모든 그림 및 GIF는 이해를 돕기 위해 직접 그린 내용들 입니다.