안녕하세요. Physics-based Humanoid Control in AI Robotics를 전공하고 있는 이민경입니다. 2020년에 잠시 추천시스템에 흥미가 생겨서 개인적으로 공부했습니다. 다양한 딥러닝, 로보틱스 관련 공부도 하면서 논문들 읽고 재구현하는 것을 좋아해요.
•
첫 리뷰 논문은 꽤 유명한 추천시스템 관련 논문인 Yehuda Koren의 "Matrix Factorization Techniques for Recommender Sytems" 입니다.
Summary
본 논문은 Recommendation System 중 Latent Factor Model based Collaborative Filtering의 일환인 Matrix Factorization에 대한 다양한 방법들을 설명한다. Matrix Factorization으로 Netflix Prize Competition에 제안한 방법과 그 결과를 소개한다.
Content
추천시스템은 크게 컨텐츠 기반 필터링(Content-based Filtering)과 협업 필터링(Collaborative Filtering)으로 구분할 수 있다. 본 논문에서 택한 Matrix Factorization은 협업 필터링의 일환이다.
여기서 협업 필터링(Collaborative Filtering) 이란, 사용자와 아이템 간의 상호 상관 관계를 분석하여 새로운 사용자-아이템 관계를 찾아주는 것으로 사용자의 과거 경험과 행동 방식에 의존한다. Domain Free 방식으로 관련 지식들이 불필요하다는 장점이 있다. 그러나 Cold Start Problem을 나타내는 한계가 존재한다.
Cold Start Problem: 문자 그대로 새로운 사용자나 새로운 아이템 등장 시, 기존의 관련된 경험 또는 행동 방식이 없기 때문에 추천이 곤란해지는 문제를 뜻한다.
협업 필터링은 근접 이웃 방법(Neighborhood Methods)과 잠재 요인 모델(Latent Factor Models)로 구분 할 수 있다. 그 중 본 논문에서 설명하는 Matrix Factorization(행렬 분해) 방법은 잠재 요인 모델(Latent Factor Model)에 해당한다.
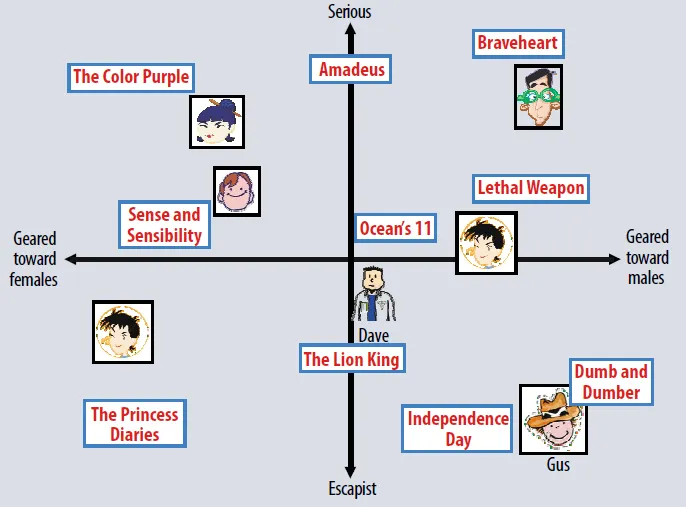
잠재 요인 모델(Latent Factor Models) : 점수 패턴에서 추론된 20-100개 정도의 요소들에 대하여 아이템들과 사용자들을 모두 특성화 하여 점수를 설명하는 방식으로, 주어진 데이터로 알 수 없는 사용자와 아이템의 숨겨진 특징(feature)들을 찾아 내고자 한다.
[Example] 이 표는 잠재 요인 모델 접근방법에 대한 설명을 나타낸 표로 남자 대 여자, Serious 대 Escapist-두 축을 사용하여 사용자들과 영화들 모두의 특성들을 표현했다.
1. Matrix Factorization
Matrix Factorization(행렬 분해) 는 아이템 점수 패턴으로부터 추론된 요소의 벡터들로 아이템들과 사용자들 모두 특성화하여 학습시키는 기법을 의미한다. 아이템과 사용자 간의 높은 상관 관계를 지닐 경우 추천하는 방법으로
•
예측 정확도와 우수한 확장성
•
다양한 실상황을 모델링 하기 위한 뛰어난 유연성 제공
이와 같은 장점을 지니는 Latent Factor Model-based Collaborative Filtering 중 하나이다.
추천 시스템의 경우 입력 데이터의 다양한 유형에 의존하는데 Matrix Factorization의 경우 추가적인 정보 통합을 허용한다. 즉 명시적 피드백을 사용할 수 없을 경우, 추천 시스템은 과거 구매 내역, 브라우저 기록, 검색 패턴, 마우스 움직임 등 사용자 행동을 관찰한 암시적 피드백(Implicit Feedback)을 사용하여 해당 사용자 선호를 유추한다.
암시적 피드백(Implicit Feedback)은 이벤트 존재 유무를 나타내므로 보통 조밀하게 채워진 Dense Matrix로 표시된다.
2. Basic Matrix Factorization Model
Matrix Factorization(행렬 분해) 모델은 사용자와 아이템을 차원(f)의 공동 잠재 요인 공간에 매핑한다. 이러한 사용자-아이템 상호 작용은 해당 공간에서 내적(inner-products)으로 모델링된다.
위의 내적 결과는 사용자와 아이템 간의 상호 작용, 즉 아이템에 대한 사용자의 전반적은 관심을 나타낸다. 이때 주어진 아이템(i)는 q_{i} 벡터로, 주어진 사용자(u)는 p_{u} 벡터로 표현한다. 이때 발생하는 주요 문제는 요인 벡터(factor vector)에 대한 각 아이템과 사용자의 매핑을 계산하는 것이다.
이와 같은 모델은 사용자-아이템 점수 행렬의 인수분해를 요구하는 특이값 분해(SVD, Singular Value Decomposition)과 매우 유사한데, 사용자-아이템 점수 행렬의 희소성으로 인해 SVD를 사용하는 것은 어렵다. 또한 비교적 적은 수로 알려진 항목들에대해 임의로 지정 할 경우 과적합(overfitting) 문제가 발생할 수 있다.
따라서 정규화된 모델을 통해서 과적합을 방지하면서 관측된 점수만 직접적으로 모델링하는 방법이 제시되었다. 요인 벡터, p_{u} & q_{i} 를 배우기 위해, 시스템은 관측된 점수 세트를 통해 정규화된 Squared Error를 최소화한다. 해당 시스템은 이전에 관찰된 점수들을 피팅하여 모델을 학습한다.
그러나 이 모델은 알려지지 않은 점수를 예측하는 것이 목적이다. 따라서 시스템은 학습된 매개 변수를 정규화하여 관찰된 데이터의 과적합을 방지해야 하고 주로 교차검증에 의해 결정되는 lambda로 정규화 범위를 제어해야 한다.
3. Learning Algorithms
위의 식을 최소화 하기 위해 2가지 방법을 제시한다.
3.1. Stochastic Gradient Descent
확률적 경사하강법(SGD)은 구현이 쉽고 빠르다는 장점이 있다. 구현 식은 아래와 같다.
우선각각의 훈련 세트에 대해, 시스템은 r_{ui}를 예측하고 예측 오차를 계산한다.
그 후 gradient의 반대 방향에서 gamma에 비례하는 크기로 매개변수를 다음과 같이 수정한다.
3.2. Alternating Least Squares
위의 식은 q_{i}와 p_{u} 모두 알 수 없기에 Convex하지 않다. 그러나 둘 중 하나를 고정할 수 있다면, 이 최적화 문제를 Quadratic하게 바꾸어 값을 구할 수 있다. 이와 같이 Alternating Least Squares (ALS) 방법은 q_{i}를 고정했다가 p_{u}를 고정하는 방식으로 동작한다. 예를 들어, 모든 p_{u}가 고정되면, 시스템은 최소 제곱법으로 q_{i}를 다시 계산한다. 이러한 방법으로 구하고자 하는 식을 최소화 할 수 있다.
일반적으로 확률적 경사하강법(SGD)이 ALS보다 빠르고 쉽지만 ALS가 유리한 2가지 경우가 있다.
1.
시스템이 병렬화를 지원하는 경우
2.
시스템이 암시적 데이터에 중점을 둔 경우
4. Adding Biases
협업 필터링에 대한 Matrix Factorization의 한 가지 이점은 데이터 측면 및 다른 애플리케이션 별 요구사항을 처리할 수 있는 유연성이다.
해당 식은 동일한 학습 프레임워크 내에서 다양한 점수 결과를 만들어 내는 사용자와 아이템 간의 상호 관계를 파악하는 것이 목적이다. 그러나 점수 결과에서 관찰된 변동의 대부분은 이러한 상호 관계와 상관없이 "사용자나 아이템 자체의 특성에서" 영향을 받으며 이를 Biases 또는 Intercepts라 칭한다.
시스템은 개별 사용자 또는 아이템의 편향(biases)이 설명할 수 있는 값의 부분을 식별하여 실제 상호 작용 부분들만 요소 모델링에 다음과 같이 적용해야 한다.
5. Additional Input Sources
앞서 언급한 Cold Start Problem 문제를 해결 해야하는 경우가 있는데 사용자에 대한 추가적인 정보 소스들을 모두 통합할 필요가 있다. 즉 사용자의 의지와 상관 없이 행동 정보를 수집할 필요가 있다.
Boolean 암시적 피드백이 있는 경우를 고려해 보자. N(u)은 암시적 선호도를 표현한 사용자(u)의 아이템 집합이다. 이와 같이 암시적으로 선호하는 항목들을 통해 시스템은 사용자 프로필을 만든다. N(u) 항목에 대하여 아이템 선호도를 보인 사용자는 다음과 같이 표현된다.
이 식을 정규화 하면
또다른 정보 소스는 인구통계와 같은 사용자 속성(User Attribute)이다.
개선된 사용자 표현과 함께 모든 Signal Sources를 통합하면 Matrix Factorization 모델은 다음과 같이 나타낼 수 있다.
6. Temporal Dynamics
지금까지 정적인 모델에 대해서만 설명하였다. 그러나 현실에서는 아이템 인식과 인기도는 새로운 것이 생길 때마다 시시각각 변하고, 고객의 성향 역시 그에 따라 변하기 마련이다. 따라서 추천 시스템은 시간에 따라 변하는 사용자-아이템의 동적 상호관계를 반영하는 Temporal Effect를 설명할 수 있어야 한다.
: 아이템 인기는 시간이 지남에 따라 변할 수 있다.
: 사용자 성향은 시간이 지남에 따라 변할 수 있다.
: 아이템에 대한 사용자 선호도 역시 시간이 지남에 따라 변할 수 있다.
7. Inputs with Varying Confidence Levels
여러 설정에서 관측된 모든 점수들이 동일한 가중치 또는 신뢰도를 받지는 못한다. 예를 들어 사용자들 중 몇몇은 일부러 특정 아이템의 점수를 낮게 줄 수 있다. 또한 암시적 피드백을 중심으로 구축된 시스템은 사용자의 정확한 선호도 레벨을 정량화 하기 어렵다.
따라서 예상되는 선호도와 함께 신뢰도 점수를 첨부하는 것이 중요하다. 이 경우 신뢰도는 행동 빈도에 따라 사용가능한 숫자 값으로 표현될 수 있는데 예를 들어, 사용자가 특정 프로그램을 시청한 시간 또는 특정 상품을 구매한 빈도 등이 신뢰도 값이 될 수 있다. 사용자의 기본 설정과는 관련 없는 일회성 이벤트가 발생할 수 있지만; 반복된 이벤트는 사용자 의견을 반영할 가능성이 더 높다.
8. Netflix Prize Competition
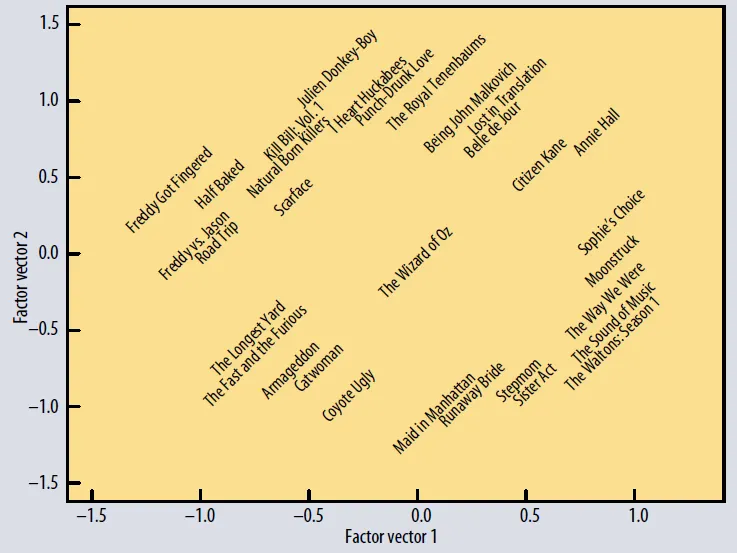
Netflix 사용자 영화 행렬을 분해하면 영화 선호도를 예측하기 위해 가장 설명적인 차원을 찾을 수 있다. 행렬 분해에서 처음 몇 가지 가장 중요한 차원을 식별하고, 새로운 공간에서 영화의 위치를 탐색 할 수 있다.
선택한 영화는 2차원 요인 벡트를 기반으로 적절한 지점에 배치 된다. 각각의 지점들은 독특한 장르들을 보여준다.
첫 번째 요소 벡터(X-axis)는 남성, 청소년 관객을 고려한 저속한 코미디와 공포 영화이고 반대편에는 진지한 음색과 강한 여성 주연이 있는 드라마나 코미디가 위치한다.
두 번째 요소 벡터(Y-axis)는 상단일 수록 독립적이고 비평가들의 찬사를 받은 기발한 영화가 위치하고 밑으로 내려올 수록 주류 공식 영화들이 위치해 있다.
Factorization을 위해 다양한 구현과 매개 변수화를 시도하였다.
행렬분해 모델의 정확성. 4개의 개별 요인 모델 각각의 평균 제곱근 오차를 보여준다.(낮을 수록 좋은 모델이다.) 요인 모델의 차원이 증가(차트에 표기된 숫자)하면 정확도가 함께 향상된다.
이 그래프는 다양한 모델과 매개변수 수가 Root Mean Squared Error에 영향을 미치는 방법과 함께 Factorization의 진화하는 구현의 성능에 미치는 영향을 보여준다.